Tag Archives: black holes

Insights from the Boundary: black holes in a magnetic universe

Posted on by
Hari Kunduri

Hari Kunduri

Following from the seminal work of Dain, a great deal is now known concerning geometric inequalities relating the area, charge, and angular momentum of axisymmetric black hole horizons in (possibly dynamical) spacetimes.  A key feature of these results is that they are quasi-local: they depend on spacetime only near the horizon itself and so are not sensitive to the asymptotic behaviour of the geometry.

For Einstein-Maxwell theory the celebrated uniqueness theorems tell us under certain conditions, that the Kerr-Newman (KN) family of solutions are the only stationary, axisymmetric and asymptotically flat black hole spacetimes. These are the model geometries that originally motivated the inequalities. However if we relax the condition of asymptotic flatness there are many other families of black hole solutions. While in general these will not contain event horizons (whose standard definitions require flat or AdS asymptotics) they still contain singularities and Killing horizons. In this paper we focussed Continue reading →

Black-hole laboratories in the era of gravitational-wave astronomy

Posted on by
Paolo Pani and Helvi Witek

Helvi and Paolo visiting Toronto during the International Conference on Black Holes at the Fields Institute last year.
Helvi is Research Fellow in the School of Mathematical Sciences at the University of Nottingham. Paolo is Assistant Professor at Sapienza University of Rome and Research Scientist at the Instituto Superior Técnico in Lisbon.

We are proud to present the completed Focus Issue on “Black holes and Fundamental Fields” one year after its first contribution has been published online.

This issue appears serendipitously at the same time as LIGO’s historic detection of gravitational waves which, simultaneously, provided us with the first direct observational evidence for the existence of black holes (BHs). We wish to take this opportunity to congratulate the LIGO/VIRGO Scientific Collaboration and everyone involved on  their breakthrough discovery!

The true excitement around this discovery arises from the fact that it marks the beginning of the long-sought-for era of gravitational-wave astronomy. As Kip Thorne recently put it, “Recording a gravitational wave […] has never been a big motivation for LIGO, the motivation has always been to open a new window to the Universe”. The outstanding observation of a BH binary coalescence — and the expectation of Continue reading →

Accreting onto almost Kerr-de Sitter black holes

Posted on by

Read the full article for free* in Classical and Quantum Gravity:
Bondi-type accretion in the Reissner-Nordström-(anti-)de Sitter spacetime
Filip Ficek 2015 Class. Quantum Grav. 32 235008
arXiv: 1509.07005
*until 30/12/15

Filip Ficek

Filip Ficek is a graduate student in Theoretical Physics at Jagiellonian University.

In spite of numerous investigations, accretion flows onto the Kerr black hole are still not fully understood, especially for radially dominated flows, where aside from a very specific case of an ultra-hard fluid, general solutions are not known. Some insight may be provided by considering a simpler problem instead, namely spherically symmetric, steady accretion in Reissner-Nordström spacetimes. It is well known that rotating Kerr black holes and charged Reissner-Nordström black holes feature similar horizon and causal structures. In fact, it is common to treat a Reissner-Nordström black hole as a toy model of an astrophysical black hole. If we also take into account the cosmological constant, we may suppose, that accretion solutions in Reissner-Nordström-(anti-)de Sitter spacetime will Continue reading →

The spin limit for cosmological black holes

Posted on by

Read the full article in Classical and Quantum Gravity (Open Access):
The area-angular momentum inequality for black holes in cosmological spacetimes
María Eugenia Gabach Clément, Martín Reiris and Walter Simon 2015 Class. Quantum Grav. 32 145006
arXiv:1501.07243

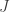In colloquial terms, the main achievement of our recent CQG article is simple to state: We have proven that the angular momentum J of an axially symmetric black hole (the Noether current) with surface area 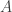A satisfies the bound.equation Walter CQG+ post

Here \Lambda is the cosmological constant –  a standard ingredient in Einstein’s Continue reading →

The curvature on a black hole boundary

Posted on by

Read the full article for free* in Classical and Quantum Gravity:
On the Bartnik mass of apparent horizons
Christos Mantoulidis and Richard Schoen 2015 Class. Quantum Grav. 32 205002
arXiv:1412.0382
*until 04/11/15

Christos Mantoulidis

Christos Mantoulidis is a graduate student in Mathematics at Stanford University.

In our latest CQG paper we study the geometry (i.e. curvature) of apparent horizons and its relationship with ADM mass.

We were motivated by the following two foundational results in the theory of black holes in asymptotically flat initial data sets (slices of spacetime) satisfying the dominant energy condition (DEC):

  1. Apparent horizons are topologically equivalent to (one or more) two-dimensional spheres.(1)
  2. When the initial data set is additionally time symmetric (totally geodesic in spacetime), the apparent horizon’s total area A is bounded from above by the slice’s ADM mass per A \leq 16\pi m^2. This is called the Penrose inequality.(2) Equality is only achieved on Schwarzschild data, whose apparent horizon is a single sphere with constant Gauss curvature.

One then naturally wonders: Continue reading →

Black holes in massive gravity

Posted on by
Eugeny Babichev

Eugeny Babichev is a CNRS researcher at the Laboratory for Theoretical Physics at Orsay. His work focuses on modified gravity theories, including their theoretical and observational issues, as well as phenomenological aspects, such as cosmology and black holes.

One of the biggest puzzles of modern physics is the present-day accelerated expansion of the Universe. The acceleration is usually attributed to the presence of a mysterious dark energy, a yet unknown substance of the Universe. Although in the framework of conventional General Relativity (GR), a cosmological constant can be added to mimic dark energy, the fine tuning required to adjust its value makes this explanation unsatisfactory. We can then ask whether a modification of Continue reading →

Gravitational lensing by black holes in astrophysics and in Interstellar

Posted on by
Interstellar's accretion disc, with and without Doppler shift.

Interstellar‘s accretion disc, with and without Doppler shift. Figure 15 a, c from “Gravitational lensing by spinning black holes in astrophysics, and in the movie Interstellar” Oliver James et al 2015 Class. Quantum Grav. 32 065001

New insights into the effects of black holes from the team responsible for the Oscar®-winning visual effects of Interstellar.

Depicting a super-massive black hole in the movie Interstellar presented a new challenge to our visual effects team at Double Negative. Luckily the Executive Producer was theoretical physicist Kip Thorne who ended up working closely with us to create a new computer code, DNGR: Double Negative Gravitational Renderer. This code traces the path of light past a spinning black hole (Kerr metric) whose immense gravity warps space and time in its vicinity. A hot disk of gas orbiting the hole appears to Continue reading →

Press release: Interstellar technology throws light on spinning black holes

Posted on by
Michael Bishop

Michael Bishop is a Senior Press Officer for IOP Publishing

The team responsible for the Oscar-nominated visual effects at the centre of Christopher Nolan’s epic, Interstellar, have turned science fiction into science fact by providing new insights into the powerful effects of black holes. In a paper published today, 13 February, in IOP Publishing’s journal Classical and Quantum Gravity, the team describe the innovative computer code that was used to generate the movie’s iconic images of the wormhole, black hole and various celestial objects, and explain how the code has led them to new science discoveries. Using their code, the Interstellar team, comprising London-based visual effects company Double Negative and Caltech theoretical physicist Kip Thorne, found that when a camera is close up to a rapidly spinning black hole, peculiar surfaces in space, known as caustics, create more than a dozen images of individual stars and of the thin, bright plane of the Continue reading →

A new algorithm for gravitational wave propagation

Posted on by
Casey Handmer and Bela Szilagyi

Casey Handmer (graduate student at Caltech) and Bela Szilagyi (senior research fellow at Caltech) discuss the finer points of null cone geometry.

Gravitational wave evolution – spectral style.

Colliding black holes create powerful ripples in spacetime. Of this we are certain. Directly detecting these ripples, or gravitational waves, is one of the hardest unsolved problems in physics. Inferring physical characteristics of black hole binaries and other gravitationally energetic events from their radiation requires accurate numerical simulation for matched filtering.

But gravitational wave simulations are typically plagued by a lack of gauge invariance. Waveform precision and validity is undermined by coordinate choice and movement. Simulations require an extraction methodology to obtain gauge invariant waveforms. These waveforms are Continue reading →

Black holes against the universe – particle and photon orbits in McVittie spacetimes

Posted on by
Brien Nolan

Brien Nolan is a Senior Lecturer in the School of Mathematical Sciences, Dublin City University

Black holes have a potential technological application that is frequently overlooked: they allow you to look at the back of your own head. This could be useful for checking that your tie is properly tucked into your shirt collar, or – perhaps more relevant for physicists – that your pony tail is straight. This technology relies on the fact that there exist circular photon orbits in all members of the Kerr-Newman-de Sitter family of spacetimes for which the parameters (mass, charge and cosmological constant) correspond to a black hole.

The question arises as to whether this characteristic feature of electro-vac Continue reading →